DR
Prova de alcance simplificada. Apenas 6 ECMUL e 3 ECADD (gás 37K) são necessários para verificar a moeda de privacidade baseada na Prova de Alcance do Compromisso Pedersen no EVM. A primeira configuração e compromisso requerem zkSNARKs, mas depois disso o custo é minimizado. Para cada geração de transação no lado do cliente, também não são necessários cálculos de ZKP.
Artigo completo com comprovante de segurança: https://eprint.iacr.org/2025/1811.pdf
Passos:
G,H,B são pontos independentes em uma curva.
Configuração única para cada provador (remetente de token)
- Experimente a ← Zq e defina a âncora pública U = aB.
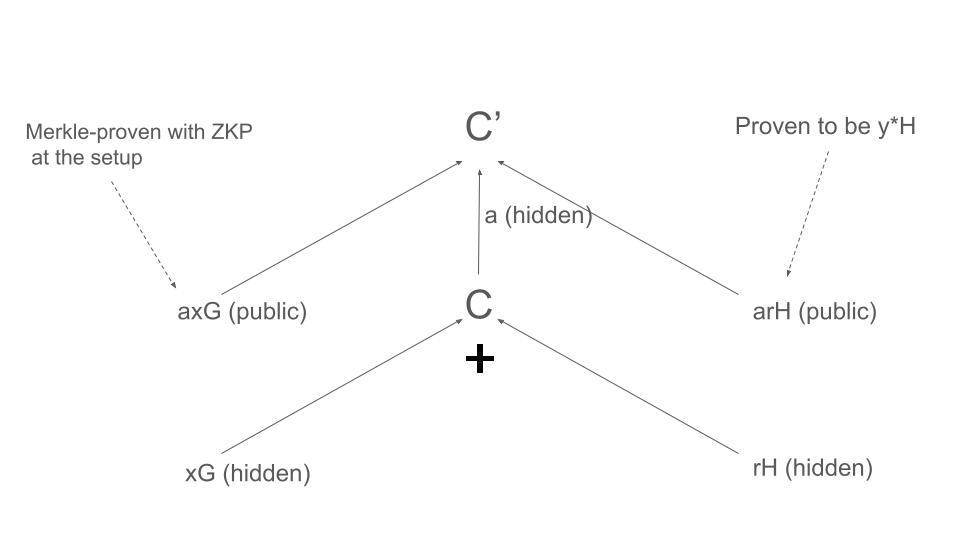
- Faça uma árvore Merkle com pontos na curva. Para cada X ∈ {1, . . . , 2 n}, defina a carga útil da folha aXG
- Com NIZK na cadeia, prove a raiz Merkle da árvore que consiste em aXG. (prova de pré-intervalo)
Provar (ao enviar um token)
- Faça o compromisso de Pedersen C = xG + rH com o valor do token x e ocultando r. (x, r, xG e rH não devem ser expostos)
- Envie C, C’ = aC, axG e sua prova Merkle, prova Chaum-Pedersen DLEQ de (U, B) e (C’, C), arH e prova do protocolo Schnorr de (arH, H)
Verifique (que C está com x em um intervalo no EVM)
1, Use Chaum-Pedersen DLEQ para verificar se (U, B) e (C’, C) têm o mesmo discreto
2. Use o protocolo Schnorr ou ECDSA para verificar se o provador consegue fazer arH a partir de H.
3. Verifique a Prova Merkle de axG na árvore de configuração.
4. Verifique C’ = axG + arH
## Por que Chaum-Pedersen DLEQ e U=aB são necessários
Se usarmos o protocolo Schnorr ou ECDSA para verificar a relação de (C’, C), um provador malicioso pode fazer C’ = yC e C = (bigX)G + rH onde y = ax/(bigX). yrH também será verificado.
Como diminuir a árvore
Fazer uma árvore com todos os números com nonces será um pouco desafiador. Fazer uma árvore de pontos por números aleatórios limitados, multiplicar folhas por números escalares e adicionar um ponto na cadeia ajudará muito, já que ninguém pode adivinhar os números aleatórios a partir dos pontos da curva da árvore.
Fontesethresear