Ethereum usa uma constante BLOB_BASE_FEE_UPDATE_FRACTION Ao atualizar a taxa base do blob a cada bloco, com a mudança proporcional na taxa calculada como:
math.exp((blob_gas_used - TARGET_BLOBS * GAS_PER_BLOB) / BLOB_BASE_FEE_UPDATE_FRACTION)
Um novo valor para essa constante foi incluído em cada EIP que altera o gás Blob de destino. Acontece que existe uma generalização simples para calcular a constante, consistente com o valor definido no EIP-4844 e EIP-7691, que seria apropriado apenas para o parâmetro BLOB (BPO) Hardforks do EIP-7892. Este cálculo generalizado de fração de atualização, também especificado aqui, é:
BLOB_BASE_FEE_UPDATE_FRACTION = round(MAX_BLOBS * GAS_PER_BLOB / (2 * math.log(1.125)))
Matematicamente, podemos expressar o valor ideal (não arredondado) como
b = \ frac {m} {2 \ ln (1.125)},
onde m é o gás máximo por bloco por bloco. Para ver por que isso generaliza o EIP-4844 e o EIP-7691, agora configuraremos as equações usadas por esses eips e derivaremos a fórmula generalizada deles.
Exposição
Definir t como o gás de blob alvo por bloco. Sob EIP-4844, o alvo está na metade do máximo: t = m/2e a taxa base do blob foi projetada para aumentar ou diminuir em um máximo de 1,125 e 1/1,125 por bloco quando o uso do blob está no seu máximo ou mínimo, respectivamente. Na Max Blob Gas consumida, a equação para a mudança proporcional na taxa se torna
e^{\ frac {mt} {b}} = e^{t/b} = 1.125.
Levando o logaritmo natural de ambos os lados e reorganizando para bentão substituindo t = m/2produz a equação especificada:
b = \ frac {t} {\ ln (1.125)} = \ frac {m} {2 \ ln (1.125)}.
Sob o EIP-7691, o BLOB_BASE_FEE_UPDATE_FRACTION é derivado como “o ponto médio entre manter a capacidade de resposta a blobs completos e sem blobs constantes”. O b Isso mantém a resposta à constante “Blobs completa” é
b_ \ text {completo} = \ frac {m – t} {\ ln (1.125)}.
O b Isso mantém a resposta à constante “sem blobs” é
b_ \ text {empty} = \ frac {-t} {\ ln \ left (\ frac {1} {1.125} \ right)},
que através da regra do logaritmo: \ ln (1/x) = -\ ln (x)torna -se
b_ \ text {empty} = \ frac {t} {\ ln (1.125)}.
O “ponto médio” (b_ \ text {completo}+b_ \ text {empty})/2 simplifica para a equação generalizada:
b = \ frac {1} {2} \ esquerda (\ frac {m – t} {\ ln (1.125)} + \ frac {t} {\ ln (1.125)} \ direita) = \ esquerda (\ frac {m – t + t} {2 \ 2 \ 2 \ 2 \ l (\ \ \ frac {m – t + t} {2 \ 2 \ 2 \ l (\ \ \ frac {m – t + t} {2 \ 2 \ \ frac {m} {2 \ ln (1.125)}.
Aplicativo
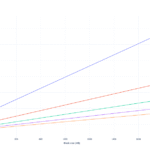
A equação generalizada fornece alterações percentuais satisfatórias em qualquer razão. A Tabela 1 descreve alguns exemplos.
| Max: Target | Completo % | Vazio % | Fator completo 1.125^k | Fator vazio 1.125^k |
|---|---|---|---|---|
| 5 {:} 4 | +4,82 \% | -17,18 \% | k = \ tfrac {2} {5} | k = -\ tfrac {8} {5} |
| 4 {:} 3 | +6,07 \% | -16,19 \% | k = \ tfrac {1} {2} | k = -\ tfrac {3} {2} |
| 3 {:} 2 | +8.17 \% | -14,53 \% | k = \ tfrac {2} {3} | k = -\ tfrac {4} {3} |
| 2 {:} 1 | +12,50 \% | -11,11 \% | k = 1 | k = -1 |
| 3 {:} 1 | +17,00 \% | -7,55 \% | k = \ tfrac {4} {3} | k = -\ tfrac {2} {3} |
| 4 {:} 1 | +19.32 \% | -5,72 \% | k = \ tfrac {3} {2} | k = -\ tfrac {1} {2} |
| 5 {:} 1 | +20,74 \% | -4,60 \% | k = \ tfrac {8} {5} | k = -\ tfrac {2} {5} |
Tabela 1. Impacto para blocos cheios e vazios em vários índices máximos: alvo com a fração de atualização generalizada.
Nota nas colunas 4 e 5 que a taxa básica muda por um fator de 1.125^konde k é uma função do gás de blob consumido g:
k (g) = \ frac {2 (g – t)} {m}.
Há uma simetria de razão complementar em torno de 2: 1. A magnitude de k é preservado quando o alvo é movido uma distância igual acima ou abaixo do ponto intermediário (m/2). Especificamente, k_ \ text {completo} (m {:} t) = -k_ \ text {empty} (m {:} (mt)) e k_ \ text {completo} (m {:} (mt)) = -k_ \ text {empty} (m {:} t)que, por exemplo, se aplica aos índices complementares 3 {:} 1 e 3 {:} 2 assim como 4 {:} 1 e 4 {:} 3.
Extensão para a normalização do gás
A equação generalizada se estende naturalmente à abordagem de normalização do gás descrita no EIP-7999. Essa abordagem dissocia a fração de atualização de qualquer limite específico de recurso por ser mais direto: normaliza o delta de gás (GT) Dividindo -o pelo gás máximo m (referido no EIP-7999 como o limite) ao atualizar a execução excess_gas. Isso permite uma única fração de atualização universal – independente de m – Ser usado para todos os recursos, independentemente de seus limites individuais.
As duas abordagens diferem apenas em quando a divisão por m ocorre. Na equação generalizada, m é colocado no numerador da fração de atualização b. Desde b O próprio é usado como denominador no expoente de atualização de taxas, (GT)/bisso efetivamente coloca m no denominador do cálculo geral.
Por fim, o fator final de mudança de taxa:
1.125^{\ frac {2 (gt)} {m}}
permanece o mesmo. No entanto, a normalização torna a arquitetura mais robusta, garantindo que o preço permaneça estável se o limite de um recurso for alterado, pois esse limite já é parte do normalizado excess_gas atualizar.
Pontos finais
O objetivo deste post foi o seguinte:
- Para expor por que A equação proposta generaliza os EIPs anteriores.
- Apresentar o efeito da equação proposta em várias taxas max: alvo, ilustrando alterações percentuais razoáveis e a simetria de proporção complementar.
- Para preparar o cenário para otimização adicional no EIP-7999. A peça final do quebra -cabeça é aproveitar as propriedades de generalização da equação, mas aplicar m em um estágio anterior, já ao atualizar o
excess_gas. - Durante o último ACDE, vários participantes reconheceram apenas as propriedades gerais após a conclusão da discussão (via bate -papo). Esta postagem pode servir como um local para uma conversa mais informada sobre o estabelecimento da equação proposta como padrão para a fração de atualização daqui para frente.
Fontesethresear