Muito obrigado a Alex, Csaba, Dmitry, Mikhail e Potuz por discussões frutíferas e revisão de redação
Resumo
A atual abordagem DAS para o Ethereum é baseada em codificação de apagamento de reed-solomão + compromissos de KZG. O novo esquema (descrito aqui propagação de bloco/blob mais rápido no Ethereum por @potuz) apresenta outro par: RLNC (codificação de rede linear aleatória) Codificação de apagamento + compromissos de Pedersen. Possui boas propriedades que podem ser usadas para considerar uma abordagem alternativa de disponibilidade de dados.
O protocolo descrito neste artigo esboça como pode ser um design de disponibilidade de dados baseado em RLC. Os conceitos usados aqui ainda não são suficientemente verificados, muito menos provaram -se formalmente. De qualquer forma, se esses conceitos estiverem corretos, o algoritmo poderá servir como base para a prototipagem. Se alguns deles estiverem incorretos, podemos ajustar o algoritmo ou pensar em ajustá -los ou substituí -los.
O raciocínio neste artigo se sobrepõe em vários pontos com o de @CsabaPostagem recente de Acelerar a escala de blob com FullDasv2 (com GetBlobs, codificação de mempool e possivelmente RLC).
Para explorar o contexto completo, incluindo comentários de raciocínio e discussão, consulte a versão estendida deste artigo: Conceito DAS alternativo baseado no rlnc – hackmd
Introdução
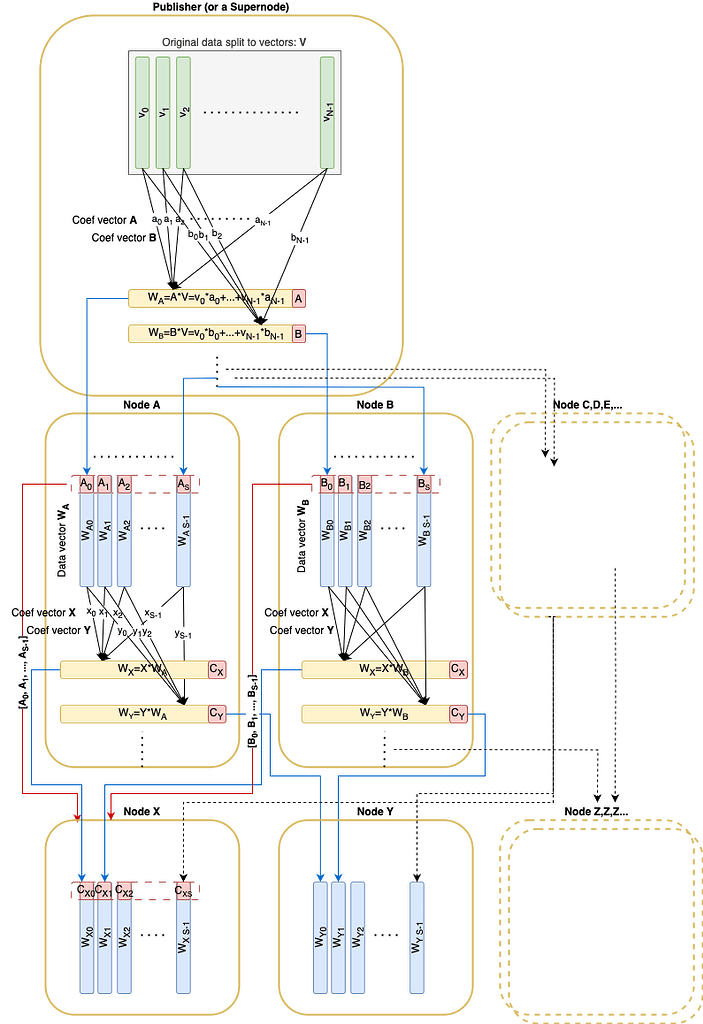
Assim como a propagação de bloco/blob de redação mais rápida no Ethereum, os dados originais são divididos em N vetores v_1, \ pontos, v_n sobre o campo \ mathbb {f} _p. Esses vetores podem ser codificados usando RLNC e comprometidos por meio de um compromisso de Pedersen (de tamanho 32 \ Times n) incluído no bloco. Qualquer combinação linear pode ser verificada, dado o compromisso e seus coeficientes associados.
Também assumimos que o coeficientes pode vir de um subcampo muito menor \ mathbb {c} _qcujo tamanho pode ser tão pequeno quanto um byte único – ou até um bit (ISENÇÃO DE RESPONSABILIDADE: A partir das últimas discussões, não está confirmado que podemos ter proteger a CE em um campo com um subcampo tão menor).
Vamos também apresentar o fator de sharding S: qualquer nó regular precisa baixar e custódia 1/s do dados originais tamanho.
Tendo um fator de fragmento fixo S Vamos pegar o número total de vetores originais N = s^2
Visão geral do protocolo breve
Um compromisso de Pedersen (tamanho 32*n) é publicado no bloco correspondente.
Durante a disseminação, cada nó recebe vetores de combinação linear pseudo-aleatória de seus pares.
- Este algoritmo descreve um não interativo abordagem onde coeficientes aleatórios são derivados de determinação do receptor
nodeIde oRREFtruque da matriz é usado (ISENÇÃO DE RESPONSABILIDADE: oRREFtruque não é estritamente provado para funcionar com segurança, no entanto, há um exemplo que pode ser a ideia inicial de prova) - Há também uma opção de fallback disponível: um interativo Abordagem onde o respondente primeiro revela seus coeficientes de origem, e o solicitante solicita a combinação linear usando coeficientes aleatórios gerados localmente.
Cada vetor de combinação linear enviado é acompanhado por vetores de base do subespaço que esse vetor foi amostrado aleatoriamente. Esses vetores de base devem formar uma matriz em forma rref. Essa condição garante que o par remoto possua vetores de base para o subespaço reivindicado.
O nó continua a amostragem até que as duas condições a seguir sejam atendidas:
- Todos os vetores de base recebidos abrangem o total NEspaço dimensional
- Pelo menos S vetores de custódia foram recebidos
Depois disso, o nó conclui a amostragem e se torna um nó ‘ativo’, que pode ser usado para amostragem por outros nós.
Observação
Os trechos de código do tipo Python abaixo são apenas para fins de ilustração, eles não devem ser compilados e executados por enquanto. Algumas funções óbvias ou semelhantes a bibliotecas não têm implementações até agora.
Tipos
Deixe os elementos do vetor de dados serem de um campo finito \ mathbb {f} _p que poderia ser mapeado para 32 bytes
type FScalar
Deixe coeficientes \ mathbb {c} _q ser de um subcampo de (ou igual a) \ mathbb {f} _p
type CScalar
Deixe um único vetor de dados ter VECTOR_LEN elementos de \ mathbb {f} _p
type DataVector = Vector(FScalar, VECTOR_LEN)
Deixe todos os dados serem cuspidos N original DataVectors:
type OriginalData = Vector(DataVector, N)
Derivado DataVector é uma combinação linear de original DataVectors. Como um vetor original é apenas um caso especial de um vetor derivado, não faremos mais nenhuma distinção entre eles.
Para validar um DataVector Contra o compromisso, seus coeficientes de combinação linear devem ser conhecidos:
type ProofVector = Vector(CScalar, N)
Há também uma sequência ligeiramente diferente de coeficientes que são usados ao derivar um novo vetor de DataVectors:
type CombineVector = List(CScalar)
Estruturas
Um vetor de dados acompanhado pelos coeficientes de combinação lineares
class DataAndProof:
data_vector: DataVector
proof: ProofVector
A única mensagem para disseminação é
class DaMessage:
data_vector: DataVector
# coefVector for validation is derived
orig_coeff_vectors: List(CombineVector)
seq_no: Int
Há uma loja efêmera para dados de um bloco:
class BlockDaStore:
custody: List(DataAndProof)
sample_matrix: List(ProofVector)
# commitment is initialized first from the corresponding block
commitment: Vector(RistrettoPoint)
Funções
Deixe a função random_coef gera um vetor de coeficiente deterministicamente aleatório com a semente (nodeId, seq_no):
def random_coef(node_id: UInt256, length: int, seq_no: int) -> CombineVector
Vamos definir funções de utilidade para calcular combinações lineares:
def linear_combination(
vectors: Sequence(DataVector),
coefficients: CombineVector) -> DataVector
def linear_combination(
vectors: Sequence(ProofVector),
coefficients: CombineVector) -> ProofVector
Função que executa operações lineares em DataVectorareia ProofVectors Simultaneamente para transformar o ProofVectors para rref:
def to_rref(data_vectors: Sequence(DataAndProof)) -> Sequence(DataAndProof)
def is_rref(proofs: Sequence(ProofVector)) -> bool
A função criando uma nova mensagem deterministicamente aleatória a partir de vetores de custódia existentes para um par específico:
def create_da_message(
da_store: BlockDaStore
receiver_node_id: uint256,
seq_no: int) -> DaMessage:
rref_custody = to_rref(da_store.custody)
rref_custody_data = (e.data_vector for e in rref_custody)
rref_custody_proofs = (e.proof for e in rref_custody)
rnd_coefs = random_coef(receiver_node_id, len(rref_custody), seq_no)
data_vector = linear_combination(rref_custody_data, rnd_coefs)
return DaMessage(data_vector, rref_custody_proofs, seq_no)
Calcula a classificação dos coeficientes dos vetores de dados. A classificação igual a N significa que os dados originais podem ser restaurados dos vetores de dados.
def rank(proof_matrix: Sequence(ProofVector)) -> int
Publicar
O editor deve cortar os dados para os vetores para obter OriginalData.
Antes de propagar o próprio dados, o editor deve calcular os compromissos de Pedersen (de tamanho 32 * N), construa e publique o bloco que contém esses compromissos.
Em seguida, o editor deve preencher a custódia com os vetores de dados (original) e suas ‘provas’, que são simplesmente elementos de uma base padrão: (1, 0, 0, ..., 0), (0, 1, 0, ..., 0):
def init_da_store(data: OriginalData, da_store: BlockDaStore):
for i,v in enumerate(data):
e_proof = ProofVector(
(CScalar(1) if index == i else CScalar(0) for index in range(size))
)
da_store.custody += DataAndProof(v, eproof)
O processo de publicação é basicamente o mesmo que o processo de propagação, exceto que o editor envia por S mensagens para um único par em uma única rodada, em vez de enviar apenas uma mensagem durante a propagação.
def publish(da_store: BlockDaStore, mesh: Sequence(Peer)):
for peer in mesh:
for seq_no in range(S):
peer.send(
create_da_message(da_store, peer.node_id, seq_no)
)
Receber
Assumindo que o bloco correspondente é recebido e o BlockDaStore.commitment é preenchido antes de receber um message: DaMessage
Derivar o ProofVector De vetores originais:
def derive_proof_vector(myNodeId: uint256, message: DaMessage) -> ProofVector:
lin_c = randomCoef(
myNodeId,
len(message.orig_coefficients),
message.seq_no)
return linear_combination(message.orig_coefficients, lin_c)
Validar
A mensagem validou primeiro:
def validate_message(message: DaMessage, da_store: BlockDaStore):
# Verify the original coefficients are in Reduced Row Echelon Form
assert is_rref(message.orig_coefficients)
# Verify that the source vectors are linear independent
assert rank(message.orig_coefficients) == len(message.orig_coefficients)
# Validate Pedersen commitment
proof = derive_proof_vector(my_node_id, message)
validate_pedersen(message.data_vector, da_store.commitment, proof)
Loja
Recebido DataVector é adicionado à custódia.
O sample_matrix está acumulando todos os coeficientes originais e assim que a classificação da matriz chegar N O processo de amostragem foi sucedido
def process_message(message: DaMessage, da_store: BlockDaStore) -> boolean:
da_store.custody += DataAndProof(
message.data_vector,
derive_proof_vector(my_node_id, message)
)
da_store.sample_matrix += message.orig_coefficients
is_sampled = N == rank(da_store.sample_matrix)
return is_sampled
is_sampled == true significa que temos (quase) 100% de certeza de que nossos pares que nos enviaram mensagens possuem coletivamente 100% das informações para recuperar os dados.
Propagar
Quando o process_message() retorna Trueisso significa que a amostragem foi bem -sucedida e a custódia é preenchida com número suficiente de vetores. A partir de agora, o nó pode começar a criar e propagar seus próprios vetores.
Estamos enviando um vetor para todos os colegas da malha que ainda não nos enviaram vetor:
# mesh: here the set of peers which haven't sent any vectors yet
def propagate(da_store: BlockDaStore, mesh: Sequence(Peer)):
for peer in mesh:
peer.send(
create_da_message(da_store, peer.node_id, 0)
)
Viabilidade
Vamos ver alguns números, dependendo de S e | \ mathbb {c} _q | (tamanho dos coeficientes) assumindo o tamanho dos dados originais de 32 MB:
| S | sizeOf(C) (bits) |
N = s^2 | Tamanho do vetor (KB) | Tamanho do compromisso (KB) | Msg Coefs Tamanho (KB) | MSG Overhead (%%) |
|---|---|---|---|---|---|---|
| 8 | 1 | 64 | 512 | 2 | 0,0625 | 0,01% |
| 8 | 8 | 64 | 512 | 2 | 0,5 | 0,10% |
| 8 | 256 | 64 | 512 | 2 | 16 | 3,13% |
| 16 | 1 | 256 | 128 | 8 | 0,5 | 0,39% |
| 16 | 8 | 256 | 128 | 8 | 4 | 3,13% |
| 16 | 256 | 256 | 128 | 8 | 128 | 100,00% |
| 32 | 1 | 1024 | 32 | 32 | 4 | 12,50% |
| 32 | 8 | 1024 | 32 | 32 | 32 | 100,00% |
| 32 | 256 | 1024 | 32 | 32 | 1024 | 3200,00% |
| 64 | 1 | 4096 | 8 | 128 | 32 | 400,00% |
| 64 | 8 | 4096 | 8 | 128 | 256 | 3200,00% |
| 64 | 256 | 4096 | 8 | 128 | 8192 | 102400,00% |
De acordo com esses números, basicamente não é viável usar este algoritmo com S \ ge 64. Se não houver opções para usar pequenos coeficientes (1 ou 8 bits), então S = 8 é o fator de sharding máximo que faz sentido devido à sobrecarga do tamanho do coeficiente. (Com S = 16a taxa de transferência mínima de download do nó seria a mesma que com S = 8.)
Prós e contras
Prós
- O tamanho total dos dados a ser disseminado, custodiado e amostrado é x1 (coeficientes+ sobrecarga que podem ser pequenos se estiverem pequenos coeficientes disponíveis) do tamanho dos dados originais (em comparação com x2 para peerdas e x4 para fulldas)
- Potencial podemos ter ‘fator de fragmento’ S Tão grande quanto 32 (ou provavelmente ainda maior com algumas outras modificações no algoritmo), o que significa que todo nó precisa baixar e custódia apenas 1/s do tamanho dos dados originais. (vs. 1/8 Na presente abordagem Peerdas: 8 colunas de 64 original)
- Os dados estão disponíveis e podem ser recuperados por ter apenas qualquer S nós honestos regulares executaram com sucesso a amostragem
- Amostragem pode ser realizada tendo qualquer S nós regulares (comparando -se ao presente DAS, onde um nó de amostragem precisa de uma variedade de colegas de sub -redes distintas do DAS)
- A abordagem ‘O que você mostra é o que você custa e serve’ (como a amostragem de sub -redes Peerdas, mas diferentemente da amostragem completa de pares). As preocupações com relação à abordagem de amostragem de pares descritas aqui
- Como nenhum fatiamento de coluna está envolvido, blobs separados podem apenas abranger vários vetores de dados originais e, portanto, o processo de amostragem pode se beneficiar potencialmente do pool de transações El Blob (também conhecido como
engine_getBlobs()) - Não há sub -redes menores que podem ser vulneráveis a ataques de Sybil
- A duplicação de dados no nível de transporte pode ser potencialmente menor devido ao fato de que um nó precisa S mensagens de qualquer colegas e o uso da codificação RLC
- RLNC + Pedersen pode ser menos consumidor de recursos que Rs + Kzg
Contras
- Compromisso e tamanho de prova crescem quadrática com coeficiente de sharding S.
- Se coeficientes menores não estiverem disponíveis (não provado ser seguro), apenas S = 8 é viável.
- Ainda preciso estimar a latência de disseminação como um nó pode propagar dados somente após o fato de concluir sua própria amostragem
- Para um caso feliz, o número mínimo de pares para amostragem é 32 (comparando a 8 em Peerdas)
Declarações a serem comprovadas
O algoritmo acima se baseia em várias declarações (ainda confusas) que precisam ser comprovadas até agora:
- Uma combinação linear válida com coeficientes aleatórios solicitados devolvidos por um super-nó prova que o nó que responde tem acesso aos dados completos (vetores suficientes para se recuperar). Esta afirmação não parece tão complicada de provar
- Se um nó completo alegar que possui vetores de base que formam um subespaço de coeficiente, se um nó solicitar um vetor aleatório deste subespaço e obter um vetor de dados válido, ele prova que o nó que responde realmente tem os vetores de base para o subspaço reivindicado. A prova pode ser uma generalização da declaração (1)
- Um CE over \ mathbb {f} _p com subcampo \ mathbb {c} _2 faz sentido e é seguro. (Isso não parece ser verdade de acordo com as últimas discussões)
- O truque com formulário de base RREF para amostragem zero-RRT funciona realmente.
(Este exemplo pode dar alguma intuição sobre a validade desta declaração) - O algoritmo descrito produz os vetores de base uniformemente distribuídos nos nós de Hones
NEspaço dimensional. Há um bem pequenoE(tipo de 1-3) de modo que o posto de vetores de base de qualquer selecionado aleatoriamenteS + Enós seriaNcom alguma probabilidade ‘muito alta’. O mesmo deve ser verdadeiro em um ambiente bizantino
Fontesethresear