Resumo
Este documento descreve um esquema hierárquico de carteira determinística que funciona com a criptografia com treliça.
Motivação
As carteiras determinísticas hierárquicas HD-Wallets tornaram-se o padrão de fato em blockchain. Como o setor de blockchain discutia um futuro pós-Quantum, gostaríamos de aplicar essa técnica às chaves em um ambiente de criptografia com treliça, pois a experiência do usuário de fazer backup de uma única frase de semente que gera zagueiro ilimitado a cada vez que uma ação é executada.
Nós nos concentramos no esquema de assinatura do Dilithium, pois foi o primeiro NIST finalizado pós-sinatura e é provável que se torne um padrão da indústria.
O desafio de adaptar a criptografia com rede a uma configuração HD é dupla. Primeiro é que a saída de um HMAC-SHA512 não pode ser usada como é para uma chave privada de treliça. Para Falcon e Dilithium
Precisamos de polinômios que formem uma “boa base” (pequenos vetores) para a treliça, e os algoritmos de geração de chaves usam a amostragem de rejeição, que não se encaixa no esquema de carteira HD sem modificação.
O segundo desafio é que, no BIP32, as chaves não endurecidas são derivadas através da adição de pontos de curva elíptica (chaves públicas) e não existe uma operação equivalente para redes: o conjunto de teclas públicas da treliça não está fechada sob adição ou multiplicação.
Abrimos o primeiro desafio neste QIP e não tentamos suportar chaves não endurecidas. É, até onde sabemos, uma questão de pesquisa aberta se esse segundo desafio pode ser superado no cenário de criptografia com treliça. As teclas não endurecidas são usadas para carteiras somente de relógio ou de auditoria e não são essenciais para o uso primário de hd-wallets, por isso não vemos isso como uma desvantagem crítica.
Especificação
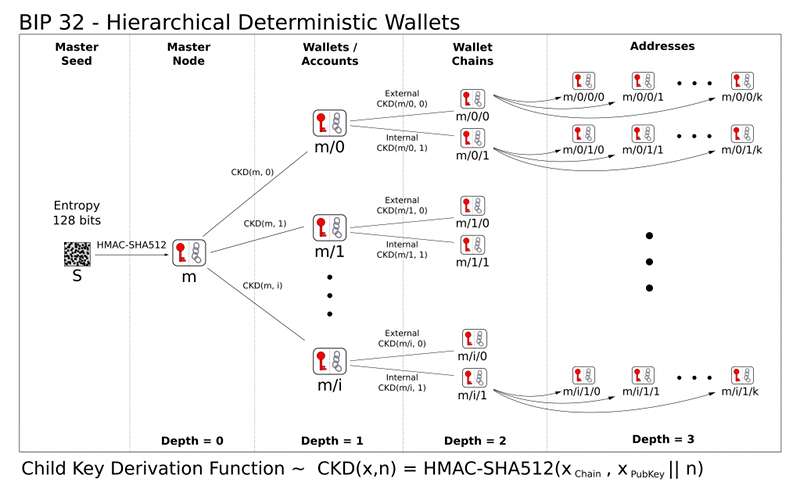
A idéia essencial é usar a saída de entropia do HMAC em cada iteração como RNG para amostragem polinomial. No BIP32, metade da saída do HMAC é usada como chave privada, diretamente como no caso “endurecido”, ou adicionado à chave privada anterior, no caso “não endurecido”. Isso funciona devido à estrutura dos algoritmos criptográficos da curva elípticos, onde a chave privada pode ser vista como apenas um número inteiro multiplicado pelo ponto do gerador no grupo da curva elípticos.
Tanto no Falcon quanto no Dilithium, os algoritmos de geração -chave consomem <= 64 bytes de entropia no processo de derivação -chave. Poderíamos simplesmente alimentar toda a saída do HMAC no processo de geração de chaves, em vez de usar a metade como a própria chave privada, mas para maximizar a interoperabilidade com as carteiras BIP44, simplesmente usamos metade da saída. Isso torna o esquema idêntico à derivação de chave endurecida no BIP32.
Esta técnica de usar a semente como o formato de chave padrão é suportada pelo NIST aqui
Implementação de referência
A implementação da carteira HD vive aqui. Testamos contra os vetores de teste gerados pelos cristais de PQ, que é a implementação de referência do Dilithium, escrito em C pelos autores do padrão.
Ambas as versões da carteira usam o Rust Library BIP39 para ir de uma “frase de semente” mnemônica para uma “semente”. Em seguida, derivamos uma “chave mestre” da semente via HMAC-SHA512 e que forma a raiz da árvore das chaves, com cada borda representando HMAC-SHA512 (r || 0x00 || l || child_index) onde l || R são os valores divididos do pai na árvore, conforme descrito no padrão BIP32.
Justificativa
Inicialmente, consideramos o uso do Falcon, pois possui chaves e assinaturas menores. Para isso, contamos com a implementação Rust-Fn-DSA de Thomas Pornin do algoritmo de assinatura do Falcon, com algumas pequenas modificações para permitir a entropia gerada externamente. Thomas Pornin foi um dos autores do padrão Falcon, e também o autor da implementação do algoritmo do algoritmo PQClean. A implementação da carteira Falcon vive aqui.
Mais tarde, chamou nossa atenção (de Thomas Pornin) que o padrão Falcon não especifica completamente o caminho da geração-chave, por isso decidimos mudar para ML-DSA (anteriormente Dilithium). Dilithium tem várias vantagens. Isso é
As desvantagens são as teclas maiores, assinaturas maiores e verificação mais lenta.
De qualquer forma, as teclas e assinaturas da treliça são todas muito maiores que as curvas elípticas, por isso teremos que pagar por mais espaço em disco.
Tanto o Dilithium quanto o Falcon requerem <= 64 bytes de entropia como entrada para o processo de geração de chaves, para que possamos simplesmente usar os primeiros 32 bytes de saída do HMAC-SHA512 como fonte de entropia. O caso de uso não endurecido não é obviamente possível com criptografia com treliça, por isso omitimos.
Em relação à segurança quântica do HMAC-SHA512, o ataque quântico primário contra as funções de hash é o algoritmo de Grover, que fornece uma aceleração quadrática na pesquisa de banco de dados não classificados (pré-imagens de hash em nosso caso). Isso corta os bits de segurança pela metade, então 512 → 256, 256 → 128, etc.
Isso se aplica a todas as funções de hash; portanto, qualquer algoritmo de hash clássico com segurança terá o mesmo problema. Por outro lado, ficou provado que o algoritmo de Grover é assintoticamente ideal; portanto, não devemos esperar que outro algoritmo quântico se faça muito melhor do que o de Grover contra uma função de hash segura.
Em contraste com as funções de hash, as assinaturas digitais das blockchains são muito mais vulneráveis a ataques quânticos, pois o algoritmo de Shor reduz a dificuldade de encontrar uma chave elíptica de uma chave privada de uma chave pública de exponencial (Rho de Pollard) para polylogarmic O (Log^3 (n)), onde n Número de bits.
Por esse motivo, estamos priorizando a garantia das assinaturas digitais contra o Quantum
Ataques e deixar as funções de hash inalteradas.
Direitos autorais
Esta especificação é liberada no domínio público.
Veja este diagrama para obter um resumo do BIP32.
Esta proposta foi publicada originalmente como uma proposta de melhoria do Quantus aqui
Fontesethresear