Canais de passagem: horizontalmente escaláveis, com privacidade aprimorada, com verificação independente, liquidez fluida e resistência robusta à censura – Página 2 – zk-s(nt)arks

1. Inicialização de teste:
   • Um cliente Bitcoin foi inicializado.
   • Gerou um novo endereço Bitcoin e confirmou 101 blocos.
   • Exibiu o saldo da carteira.
2. Gerenciamento de estado do canal:
   • Criado um estado inicial do canal com saldos e uma raiz Sparse Merkle Tree (SMT).
   • Foram aplicados dados de transição, incluindo alterações de saldo e atualizações de nonce.
3. Hashing de estado:
   • Os estados inicial e atualizado foram criptografados usando primitivas criptográficas, com cálculos de hash detalhados registrados.
4. Operações da árvore Merkle:
   • A árvore Merkle foi atualizada com o novo estado.
   • Uma prova Merkle foi gerada e verificada com sucesso.
5. Transação OP_RETURN:
   • Uma transação OP_RETURN foi criada, assinada e enviada.
   • O ID da transação e os detalhes do bloco confirmado foram exibidos.
6. Conclusão do teste:
   • O teste foi concluído com êxito, com aprovação em todas as afirmações.

Descrição:

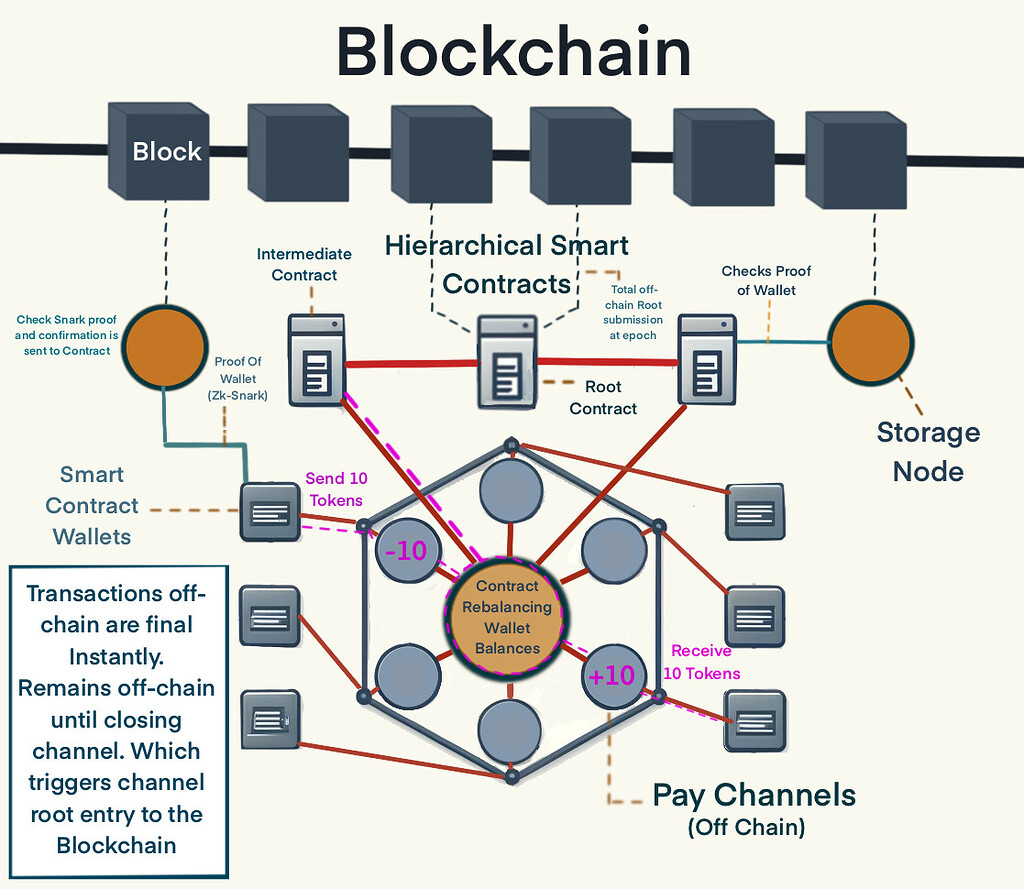
Esta captura de tela captura um marco crítico para o protocolo Overpass Channels – um teste de integração ponta a ponta que mostra sua capacidade de gerenciar com segurança transições de estado e ancorar dados diretamente no Bitcoin.

• O protocolo cria um ambiente de camada 2 confiável para Bitcoin, aproveitando provas criptográficas e Sparse Merkle Trees (SMTs) para gerenciamento de estado escalonável e verificável.

• Este teste demonstra:

• Transições de estado bem-sucedidas entre participantes do canal.

• Hashing de estado criptográfico e verificação de provas.

• Ancoragem segura do estado do canal ao Bitcoin através de transações OP_RETURN.

• Resultado: O teste passou perfeitamente, validando o processo de ancoragem confiável e o potencial de escalabilidade dos canais Overpass.

Isto marca um passo significativo para permitir aplicações baseadas em Bitcoin escalonáveis, privadas e imutáveis.

NOVOS DOCUMENTOS DE LANÇAMENTO:
#1 Documentação de desenvolvedores e pesquisadores: Viaduto
Estrutura com Composição Matemática Perfeita (PMC)

#2 Bitcoin nativo fora da cadeia: uma estrutura matemática para
Protocolo True Layer 2 Value Overpass

O diagrama acima mostra como com o Overpass consegui resolver efetivamente o Trilema alcançando a “Composibilidade Matemática Perfeita”, que foi considerada talvez apenas teoricamente possível e a maioria considerada impossível. Eu não estava procurando por isso especificamente. Como dimensionar em geral… Consegui identificá-lo enquanto o Overpass exibia certas propriedades principais, mas nem todas idealmente e então fiz alguns ajustes que pareciam intuitivos no protocolo e então percebi que era único, fiz algumas leituras e descobri que já havia um nome para ele… PMC

Isso abre um paradigma totalmente novo para Web3

DR

A arquitetura do Viaduto se destaca por transições de estado baseadas em caminhada aleatória combinado com Integração hierárquica de Pedersonpermitindo a verificação O(1) e a resistência quântica explícita contra os algoritmos de Grover e Shor, mantendo transições de estado eficientes entre camadas hierárquicas.

Fundo

Os sistemas tradicionais de atualização de estado exigem verificação completa do caminho Sparse Merkle Tree (SMT), resultando em complexidade O (log n). Estes introduzem desafios de escalabilidade quando aplicados a sistemas hierárquicos como o Overpass.
A verificação de passeio aleatório permite operações em tempo constante, ao mesmo tempo que complica diretamente os vetores de ataque quântico por meio da integração estrutural com os caminhos de autenticação Pederson.

Proposta

Implementos de viaduto:

1. Transições de estado de caminhada aleatória com Pedersen Integração:

   Onde P(h) representa o Pedersen caminho de autenticação

2. Resistência ao Ataque Quântico:

   • Passeios aleatórios realizados na estrutura SMT com Pedersen integração:

     H_{\text{novo}} = H_{\text{antigo}} \oplus RW(s, k) \otimes P(h)

   • Complica explicitamente o algoritmo de Grover ao exigir:

     O(2^{n/2}) \vezes O(2^{P(h)}) = O(2^{n/2 + P(h)})

   • Derrota o algoritmo de Shor evitando a estrutura de grupo cíclica:

     \nexists \text{ } g^x \text{ mod } p \text{ estrutura em } RW(s,k) \otimes P(h)

Vantagens

1. Resistência ao Ataque Quântico:
   • Algoritmo de Grover: as iterações necessárias aumentam exponencialmente
   • Algoritmo de Shor: Nenhum grupo cíclico subjacente para atacar
2. Geração Eficiente de Provas:
   • Tamanho e geração de prova em tempo constante:
     • Posição inicial → Passeio aleatório + Pedersen → Posição final
3. ** Pedersen Benefícios de integração**:
   • Camada adicional de resistência quântica
   • Mantém a complexidade da verificação O(1)
4. Composição Matemática Perfeita:
   • As atualizações de estado integram-se perfeitamente à verificação em tempo constante

Comparações

1. Sistemas Tradicionais Resistentes a Quânticos:
2. Sistemas de Grupo Cíclico:
3. Ultrapassar:
   • Combina resistência estrutural e computacional:

     \text{Verificar}(RW(s,k) \otimes P(h)) = O(1)

     \text{Ataque Quântico} = O(2^{n/2 + P(h)})

Aplicativos

1. Sistemas de Estado Pós-Quantum:
   • Explicitamente resistente a ataques quânticos conhecidos
2. Autenticação Hierárquica:
3. Protocolos à prova de futuro:
   • Resistência estrutural a algoritmos quânticos

Conclusão

Verificação baseada em caminhada aleatória do viaduto com Pedersen a integração atinge complexidade O(1) ao mesmo tempo que fornece resistência explícita aos algoritmos de Grover e Shor. A combinação de resistência quântica estrutural e computacional, sem sacrificar o desempenho, representa um avanço significativo no projeto de sistemas de transição de estado resistentes a quânticos.