Queremos motivar o uso de códigos sem taxas, particularmente a codificação de rede linear aleatória (RLNC), por meio de uma abordagem de amostragem sob demanda, em vez de amostragem de um conjunto codificado fixo, como feito nos métodos DAS predominantes, como Celestia, SPAR ou Peer/Full DAS, do ponto de vista da eficiência da amostragem.
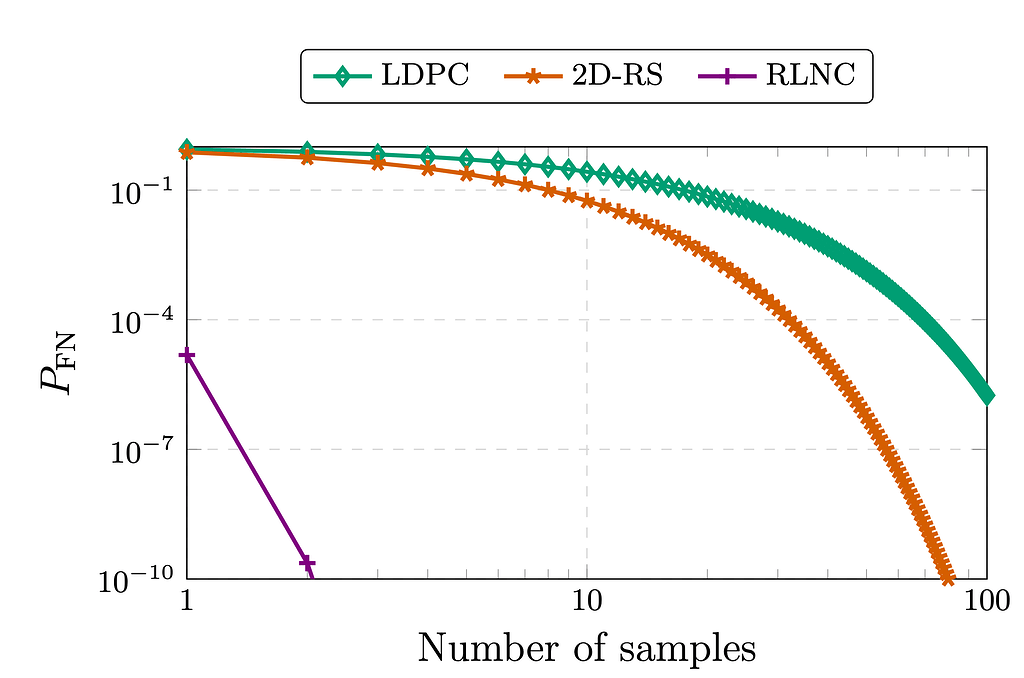
A motivação original para o uso da codificação para DAS foi que, sob anonimato, a amostragem de dados não codificados apenas diminui a probabilidade de falso negativo (um verificador conclui que os dados estão disponíveis mesmo que não estejam) linearmente com o número de amostras tomadas como 1 - s/k para amostras retiradas de k pedaços não codificados. Agora, se aplicarmos um (n,k) Código RS, por exemplo, a probabilidade de falso negativo para s amostragens (sem reposição) diminui mais rapidamente do que (k-1/n)^s
Ao empregar codificação de taxa fixa, o verificador (cliente leve) restringe-se inerentemente à amostragem de um conjunto pré-codificado de n símbolos. Olhando para a probabilidade de falso negativo acima para amostragem a partir de dados codificados de taxa fixa, a questão que surge naturalmente é: por que não tornar o n tão grande quanto possível, de modo que a probabilidade de falso negativo seja suficientemente baixa, mesmo para um pequeno número de amostras? Existem várias desvantagens nisso, incluindo:
-
Os códigos usados aqui são geralmente códigos como códigos RS que têm limites inerentes à magnitude do
nbem como as possíveis combinações de(n,k). -
o armazenamento e o custo computacional no produtor de dados aumentariam inadvertidamente junto com os custos de largura de banda para dispersão de dados de amostragem para nós de custódia, como por exemplo em PeerDAS.
Uma solução natural para este problema seria criar amostras sob demanda para evitar gargalos de armazenamento e dispersão, o que naturalmente nos leva a considerar códigos sem taxa, pois podem ser vistos como códigos separáveis por distância máxima (MDS) no limite para grandes n. RLNC é um exemplo de código sem taxa que constrói pacotes codificados formando combinações lineares aleatórias dos dados originais.
A amostragem sob demanda de um código como RLNC fornece uma probabilidade falsa negativa de (1/q)^s onde q denota a cardinalidade do campo para os coeficientes de codificação. A descrição completa de um desses protocolos é fornecida neste artigo: Da indexação à codificação: um novo paradigma para amostragem de disponibilidade de dados
Probabilidade de um falso negativo (a indecodificação da carga útil subjacente não é detectada) para amostragem de dados codificados (ver (1), (2)).
Outra desvantagem dos dados codificados com taxa fixa é que as amostras são individualizadas, o que abre espaço para procedimentos caros de reparo. Para códigos RS 1D, conforme usado em PeerDAS, por exemplo, a perda de uma única célula de um blob codificado RS requer o download do equivalente a um blob inteiro para reconstruir os dados devido às propriedades de localidade ruins dos códigos RS. Assim que os códigos tensores forem introduzidos, isso melhorará, mas um código não estruturado como o RLNC também pode fornecer uma versão mais descentralizada de custódia distribuída,
Um protocolo para custódia descentralizada usando RLNC foi proposto por @Nashatyrev mostrando propriedades favoráveis na largura de banda de reparo, bem como na sobrecarga de disseminação e armazenamento.
(1) Al-Bassam, Mustafa, et al. “Provas de fraude e disponibilidade de dados: detecção de blocos inválidos em clientes leves.” Conferência Internacional sobre Criptografia Financeira e Segurança de Dados. Berlim, Heidelberg: Springer Berlin Heidelberg, 2021.
(2) Yu, Mingchao, et al. “Árvore merkle codificada: Resolvendo ataques de disponibilidade de dados em blockchains.” Conferência Internacional sobre Criptografia Financeira e Segurança de Dados. Cham: Springer International Publishing, 2020.
Fontesethresear