Agradecimentos especiais a Gary, Dragan, Milos e Carl pelo feedback e avaliação!
Ethereum EIP-7928: Listas de acesso em nível de bloco (BALs) abre a porta para paralelização perfeita de transações. Uma vez que a pegada de leitura/gravação de cada transação é conhecida antecipadamente, a execução não depende mais da ordem: todas as transações podem ser executadas de forma independente.
Mas mesmo com perfeita independência, agendamento pode importar.
Se respeitarmos a ordem natural dos blocos em vez de reordenarmos as transações, poderemos acabar com núcleos ociosos aguardando uma única transação grande. A solução para isso seria anexar gas_used valores para a lista de acesso em nível de bloco, conforme apresentado em Chamada de grupo EIP-7928 # 6 e especificado aqui.
Alguém poderia aproximar o
gas_usedvalores utilizando o limite de gás de transação já disponível; no entanto, isso pode ser facilmente enganado. Outras heurísticas, como o número de entradas BAL para uma determinada transação ou a diferença de saldo do remetente, podem produzir resultados ainda melhores, mas trazem complexidade adicional.
Confira esta ferramenta que permite visualizar blocos de pior caso para um determinado limite de gás de bloco e número de núcleos, comparando Agendamento de lista ordenada com Agendamento ganancioso com reordenamento.
1. Configuração
Modelamos um bloco como um conjunto de “trabalhos” (transações) indivisíveis com cargas de trabalho de gás:
| Símbolo | Significado |
|---|---|
| G | Gás total do bloco (aqui 300\texto{M}) |
| G_T | Limite de gás por transação (EIP-7825, 2^{24}=16,78\texto{M}) |
| g_i | Gás da transação (i), com 0 < g_i \le G_T |
| g_{\máx} | Maior transação do bloco \le G_T |
| n | Número de núcleos |
| C | Makespan: gás total processado pelo núcleo mais movimentado |
Comparamos dois agendadores:
- Ganancioso (Reordenação permitida): as transações podem ser reorganizadas livremente para equilibrar o gás total entre os núcleos.
- Agendamento de lista ordenada (OLS): as transações permanecem na ordem natural de bloqueio; cada nova transação vai para o primeiro núcleo disponível.
2. Limite inferior: agendamento ganancioso com reordenamento
Mesmo o agendador ideal não pode fazer melhor do que:
C_* \ge \max\Big(\frac{G}{n}, g_{\max}\Big)
O termo G/n representa o carga média por núcleo;
g_{\máx} garante que nenhum núcleo possa ser atribuído menos do que a maior transação única.
3. Agendamento de lista ordenada (OLS)
Para ordem de bloco natural, o agendamento de lista vinculada de Graham fornece:
\boxed{C_{\text{OLS}} \le \frac{G}{n} + \Big(1-\frac{1}{n}\Big) g_{\max}}
Intuitivamente:
- O primeiro termo G/n é o trabalho médio ideal por núcleo.
- O segundo termo é um efeito de cauda: uma transação quase máxima pode ser agendada por último, forçando um único núcleo a continuar funcionando enquanto outros estão ociosos.
Substituindo g_{\máx} com a tampa G_T:
\boxed{C_{\text{OLS}} \le \frac{G}{n} + \Big(1-\frac{1}{n}\Big) G_T}
Este é o limite superior para execução de blocos ordenada e sem conflitos.
3.1. Dois Regimes
Deixar R = G / G_T: o número de transações de tamanho máximo que cabem em um bloco.
Para G = 300\texto{M} e G_T = 16,78\texto{M}obtemos R \aproximadamente 17,9.
Esta proporção define duas regiões distintas:
Caso A: Carga média ≥ transação única n\le R
Aqui, muitas transações preenchem o bloco, portanto a cauda aditiva é importante.
\begin{aligned} C_* &\ge \frac{G}{n}, \end{aligned}
\begin{aligned} C_{\text{OLS}} &\le \frac{G}{n} + \Big(1-\frac{1}{n}\Big)G_T \end{aligned}
Limite superior de sobrecarga relativa:
\boxed{\Delta_A(n) \le \frac{(n-1)G_T}{G}}
Caso B: carga média n > R
Com muitos núcleos, a carga de trabalho média de cada um é menor do que uma única transação.
\begin{aligned} C_* &\ge G_T, \end{aligned}
\begin{aligned} C_{\text{OLS}} &\le \frac{G}{n} + \Big(1-\frac{1}{n}\Big)G_T \end{aligned}
Limite superior de sobrecarga relativa:
\boxed{\Delta_B(n) \le \frac{1}{n}\Big(\frac{G}{G_T}-1\Big)}
Como n \to \inftyambos os escalonadores convergem para C = G_T: apenas uma transação domina a execução.
4. Ganancioso com reordenamento
Em contraste com Agendamento de lista ordenadao Ganancioso com reordenamento O modelo assume que as transações podem ser reordenadas livremente para minimizar o lucro total.
Isso representa a situação ideal em que o validador conhece antecipadamente todos os gases de transação usados e os atribui de maneira ideal aos núcleos para equilibrar a carga total.
O algoritmo Greedy preenche cada núcleo sequencialmente com a maior transação restante que cabe, produzindo um equilíbrio quase perfeito, exceto por um pequeno restante.
Formalmente:
\boxed{ C_{\text{ganancioso}}^{\max} = \begin{cases} r, & q = 0,\\(6pt) \displaystyle \max\!\Big(\lceil q/n \rceil\,G_T,\;\lfloor q/n \rfloor\,G_T + r\Big), & q \ge 1, \end{cases} }
com
q = \left\lfloor \frac{G}{G_T} \right\rfloor, \quad r = G – q \, G_T
Isto representa o limite superior no gás total executado pelo núcleo mais ocupado sob reordenamento perfeito:
- \lfloor q/n \rfloor G_T: carga de linha de base uniforme por núcleo.
- R: resto que não pode ser distribuído uniformemente.
5a. Exemplo prático G = 300\texto{M}; G_T = 16,78\texto{M}
| Núcleos n | Caso | Limite inferior C_* (Mgás) | Pior caso ganancioso C_{\text{ganancioso}}^{\max} (Mgás) | Limite superior do OLS (Mgas) | Despesas gerais vs gananciosos |
|---|---|---|---|---|---|
| 4 | UM | 75,00 | 83,90 | 87,58 | +4,4% |
| 8 | UM | 37,50 | 50,34 | 52.18 | +3,7% |
| 16 | UM | 18h75 | 33,56 | 34,48 | +2,7% |
| 32 | B | 16,78 | 16,78 | 25,63 | +52,7% |
Interpretação
- Até 17 núcleos, Ethereum opera em Caso A.
O desequilíbrio do escalonador ordenado cresce aproximadamente linearmente com n porque cada núcleo adicional reduz G/nmas o termo final (1-1/n)G_T permanece constante. - Sob um limite de gás de bloco de 300 milhões e com mais de 17 núcleos, Caso B começa: adicionar mais núcleos não ajuda mais: o limite por transação G_T torna-se o gargalo.
- A cauda irredutível do pior caso é limite de gás de uma transação.
Mesmo com a paralelização perfeita, você ainda pode acabar esperando que uma transação full-cap seja executada sozinha. - C_{\text{OLS}} sempre acrescenta um inevitável (1 – 1/n)G_T cauda.
- Dimensionamento ideal \sim G/n só é alcançável com reordenamento (Ambicioso linha de base).
- Para configurações realistas (≤ 16 núcleos), OLS pode aumentar a carga por núcleo do pior caso em 16–84%em comparação com o melhor cenário e dependendo n.
5b. Exemplo prático G = 268\texto{M}; G_T = 16,78\texto{M}
| Núcleos (n) | Caso | Carga média (S/n) (Mgás) | Pior caso ganancioso (C_{\text{ganancioso}}^{\max}) (Mgás) | Limite superior do OLS (Mgas) | Despesas gerais vs gananciosos |
|---|---|---|---|---|---|
| 4 | UM | 67.11 | 67.11 | 79h30 | +18,2% |
| 8 | UM | 33,56 | 33,56 | 48,26 | +43,8% |
| 16 | UM | 16,78 | 16,78 | 31.33 | +86,7% |
| 32 | B | 8.39 | 16,78 | 24,62 | +46,7% |
Interpretação
- Até n = 16 núcleos, estamos em Caso A (\text{média} \ge G_T).
O desequilíbrio do OLS cresce aproximadamente linearmente com njá que a cauda aditiva (1 – \tfrac{1}{n}) G_T permanece constante. - Além n > 16, Caso B começa: o limite Greedy satura em uma transação full-cap (G_T), mas OLS continua a adicionar o termo final, criando um \sim47% sobrecarga.
- Comparado com o anterior 300\texto{M} exemplo de gás, definindo o limite de gás de bloqueio para um múltiplo exato de G_T suaviza pequenos efeitos de cauda, mas mantém o mesmo comportamento geral: a execução ordenada ainda fica atrás do Greedy limitado por aproximadamente 20–90%dependendo do número de núcleos.
Indo com gas_used valores no BAL desbloqueiam o agendamento com reordenação. No entanto, o limite do gás de bloqueio determina a eficiência com que o sistema se comporta nos piores cenários em comparação com Agendamento de lista ordenada. Os validadores poderiam definir estrategicamente o limite de gás para o limite em n \vezes G_T para aproveitar totalmente os benefícios do reordenamento de transações.
Com n\to\infty o agendamento ganancioso com reordenação produz outro 2x no escalonamento, em comparação com o OLS.
Resumindo:
- OLS é dimensionado linearmente, mas sofre sobrecarga de até +80% para ≤16 núcleos.
- Ganancioso com reordenamento atinge uma escala quase ideal, limitada apenas por G_T.
- Incluindo
gas_usedos valores nos BALs poderiam duplicar a eficiência paralela, mas acrescentam complexidade.
Na prática, os validadores Ethereum não são um grupo homogêneo com especificações de hardware idênticas. Além disso, não está totalmente claro quantos núcleos estão disponíveis para execução, tornando as otimizações mais desafiadoras e menos eficazes. Em vez de enfrentar um tempo de execução do pior caso escalonado passo a passo, OLS garante um pior caso que escala linearmente com o limite de gás do bloco. Dado o cenário heterogêneo do validador e a incerteza em torno do número de núcleos disponíveis para execução, incluindo gas_used valores podem adicionar complexidade sem benefício garantido, tornando Agendamento de lista ordenada a linha de base mais previsível para o caminho de expansão do Ethereum.
6. Apêndice
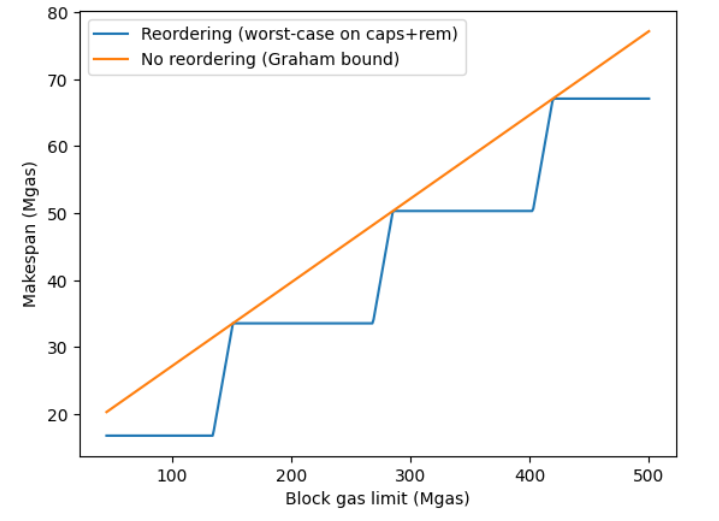
Pior caso C de OLS (laranja) vs. Ganancioso + Reordenação (azul) acima dos limites crescentes de gás de bloqueio usando 8 threads:
Comparação de agendamento do pior caso para limite de gás de bloco de 60M e 4 threads:
Fontesethresear